import io.data2viz.axis.*
import io.data2viz.color.*
import io.data2viz.geom.*
import io.data2viz.scale.*
import io.data2viz.viz.*
import kotlin.math.ln
import kotlin.math.round
var superscript = "⁰¹²³⁴⁵⁶⁷⁸⁹"
val margins = Margins(40.5, 30.5, 50.5, 50.5)
val chartWidth = 960.0 - margins.hMargins
val chartHeight = 500.0 - margins.vMargins
// linear scale domain 0..100 is mapped to 0..width
val xScale = Scales.Continuous.linear {
domain = listOf(.0, 100.0)
range = listOf(.0, chartWidth)
}
// log scale
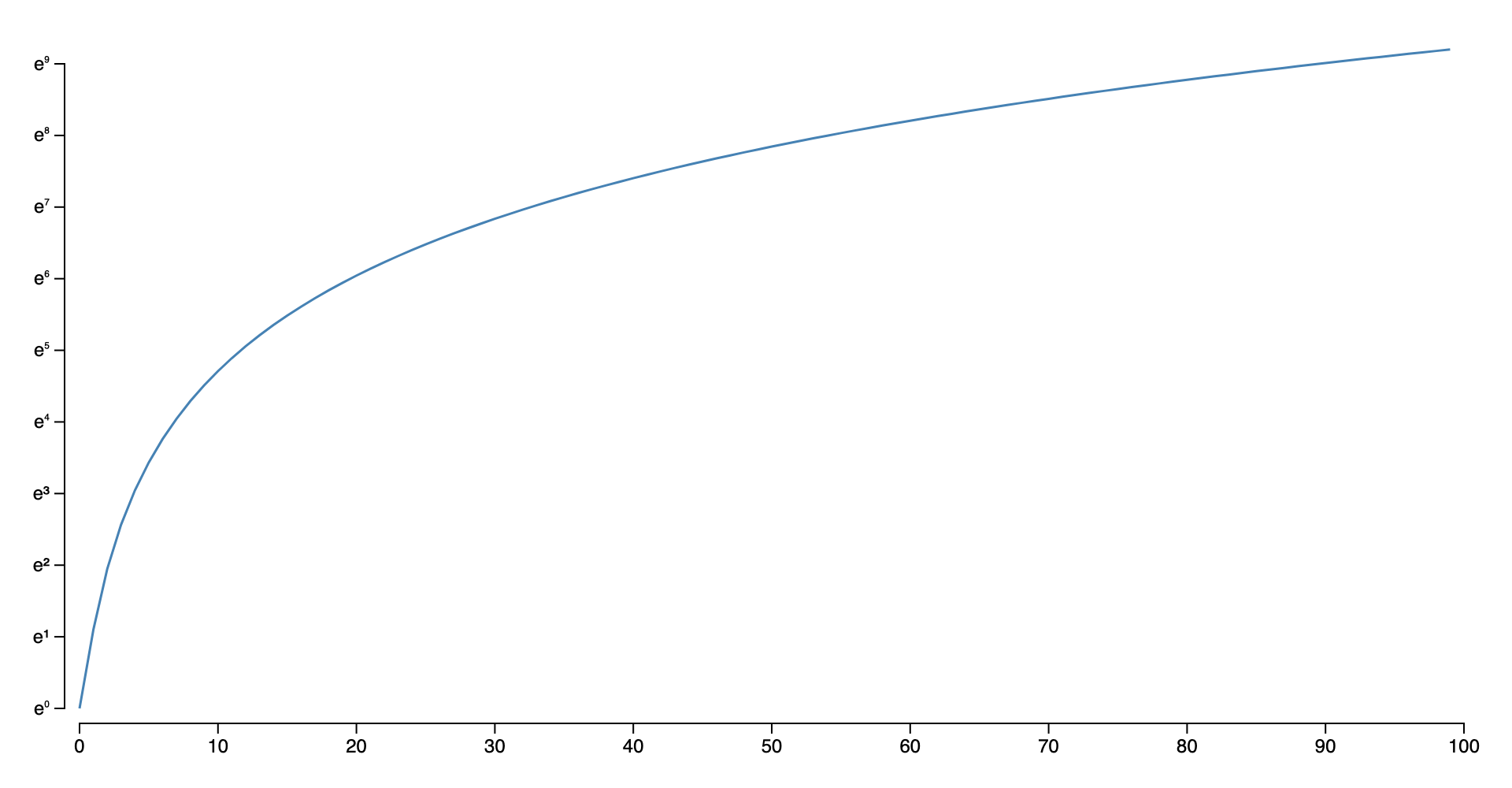
val yScale = Scales.Continuous.log (kotlin.math.E) {
domain = listOf(kotlin.math.exp(0.0), kotlin.math.exp(9.0))
range = listOf(chartHeight, .0) // <- y is mapped in the reverse order (in SVG, javafx (0,0) is top left.
}
// the mathematical function
val functionToPlot = { x:Double -> x * x + x + 1}
//100 points to define the curve
val points = (0 until 100).map { i -> Point(i.toDouble(), functionToPlot(i.toDouble()))}
fun main() {
viz {
size = size(960, 500)
group {
transform {
translate(x = margins.left, y = margins.top)
}
group {
transform {
translate(x = -10.0)
}
axis(Orient.LEFT, yScale) {
tickFormat = { "e${superscript[round(ln(it)).toInt()]}" } // <- specific formatter to add exponents (ex: e¹)
}
}
group {
transform {
translate(y = chartHeight + 10.0)
}
axis(Orient.BOTTOM, xScale)
}
group {
path {
fill = null
strokeColor = Colors.Web.steelblue
strokeWidth = 1.5
moveTo(xScale(points[0].x), yScale(points[0].y))
(1 until 100).forEach {
lineTo(xScale(points[it].x), yScale(points[it].y))
}
}
}
}
}.bindRendererOnNewCanvas()
}